ええ?なにこのポスト?
ある関数fの微分を計算するとは、わりと簡単なルールを守りながら繰り返す操作になっていますので、計算機の力が疑いなく利用したいです。このポストで微分可能なプログラミングについての理解を深めたいと思います。
具体的に、機械学習への応用を考えながら下記の点について紹介したいと思います:
- 数学的な符号を理解・表現する
- Katorovich(計算)グラフ
- 微分アルゴリズムの一覧
- 自動微分(Auto-differentiation):ボトムアップ型(Forward)・トップダウン型(Backward)の違い
- 実装・機械学習における考慮
リソース
- What is Automatic Differentiation?ものすごくいい、まずはこれ!
- Rall, Louis B. (1981). Automatic Differentiation: Techniques and Applications. Lecture Notes in Computer Science. 120. Springer. ISBN 978-3-540-10861-0.
- Swift Differentiable Programming Manifesto
- Numerical, symbolic, Automatic differentiation
- Toronto University CSC321スライド
背景
微分を計算することにおいて、まず「ある関数fに対して、fを表す符号を理解する、コンピューターに適切なフォーマットで表す」という問題が中心になる。
数学的な符号を理解・表現する
厳密には、Factorable function またはCodeable functionという定義を使う。

例を見てみましょう:
ある関数 f(x, y) に対して、下記のオペレーションのシーケンスが生成できます:
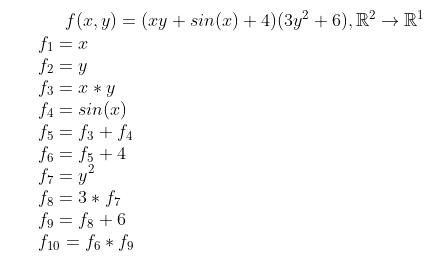
例の場合:
- 入力が二つありますのでn = 2, 出力が一つありますのでm = 1
- f1 = x とf2 = y により条件1)を満足する
- f10(最後のタームで)により唯一の結果を計算できるので条件2)を満足する
- f3からf10まで簡単な計算関数・三角関数のg({fi}))により次のステップを計算できるので、条件3)を満足する。また、関数gのセットを Λと呼ぶ。
- 簡単な数学的なオペレーションをΛが普通に、どのプログラミングでも定義されている
更に、上記のシーケンスを使って、Kantorovichグラフが作れる。
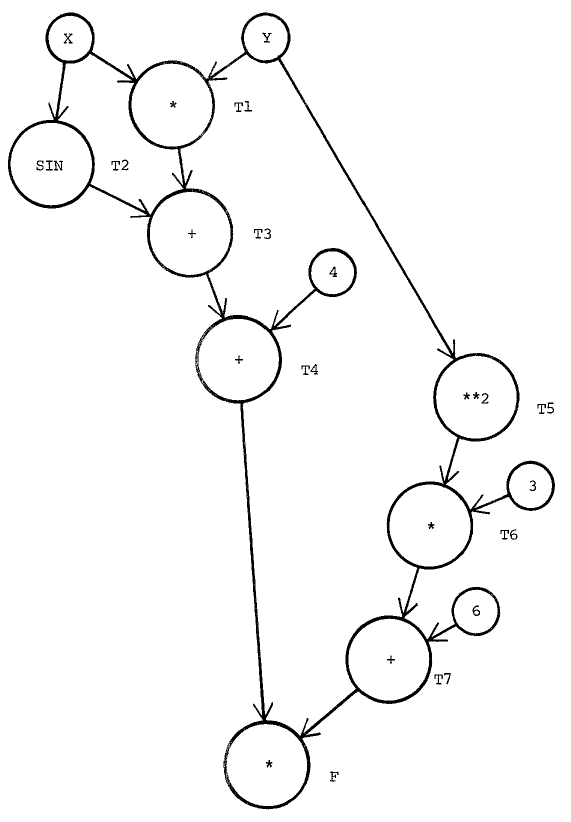
上記のグラフの中、ノードは三種類ある:
- 出力だけ:入力の変数(x, y)かまた常数c。
- 出力・入力どっちでもある:中間の計算結果。
- 入力だけ:最終結果
以上のシーケンス・グラフを使って、どのような複雑な関数であっても理解しやすいグラフ、パソコンが理解できるシーケンスで表せる。
微分を計算するアルゴリズム一覧
微分を計算するアルゴリズムは、
- 数値微分法 (Numerical Differentiation)
数字から微分を値を求める手法です。一番有名・簡単なのは差分商です。
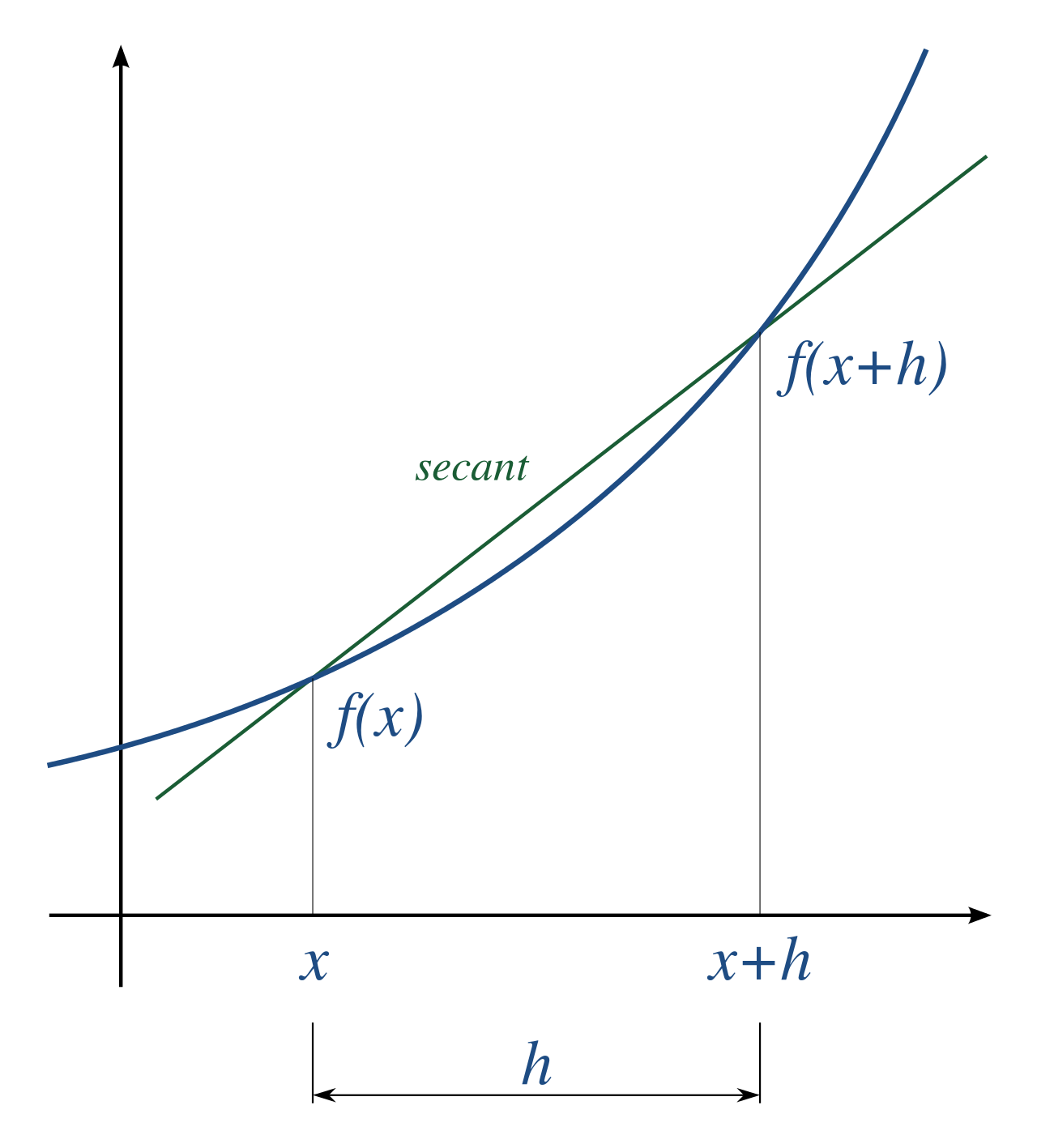
利点として実装でも簡易にできる上に、N次の導関数でも求めらる。更に、関数の本体を知らずに、サンプルデータでも計算できます
デメリットとして誤差が大きくて、特に、hが小さくなると、直線の精度は上達しますが、フロート計算の精度が落ちてしまいますので、最適のHの値を見つけるのが難しい。
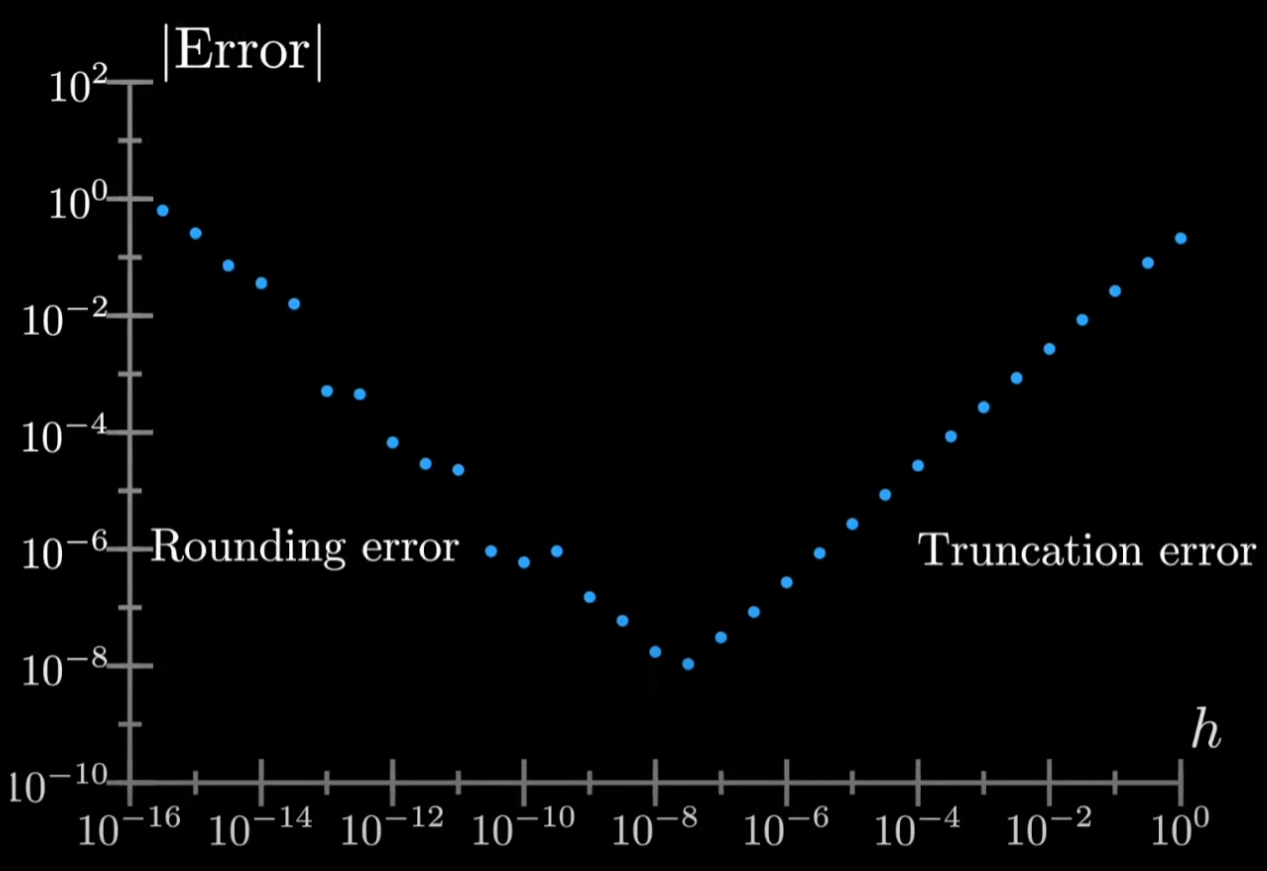
更に問題的なのは、計算量がO(n)であること。機械学習においてパラメーターの数の正比例と意味しているので効率が悪いです。
- 符号微分 (Symbolic Differentiation)
符号を微分の法則で一つ一つ展開し最後にマージして、数学的な表現を手に入れられる。手で式を計算すると同じ流れになります。MATLABとMathematicaはこのアプローチを使っている。
利点として結果は精確であり、人間の考えかたに似っていること。
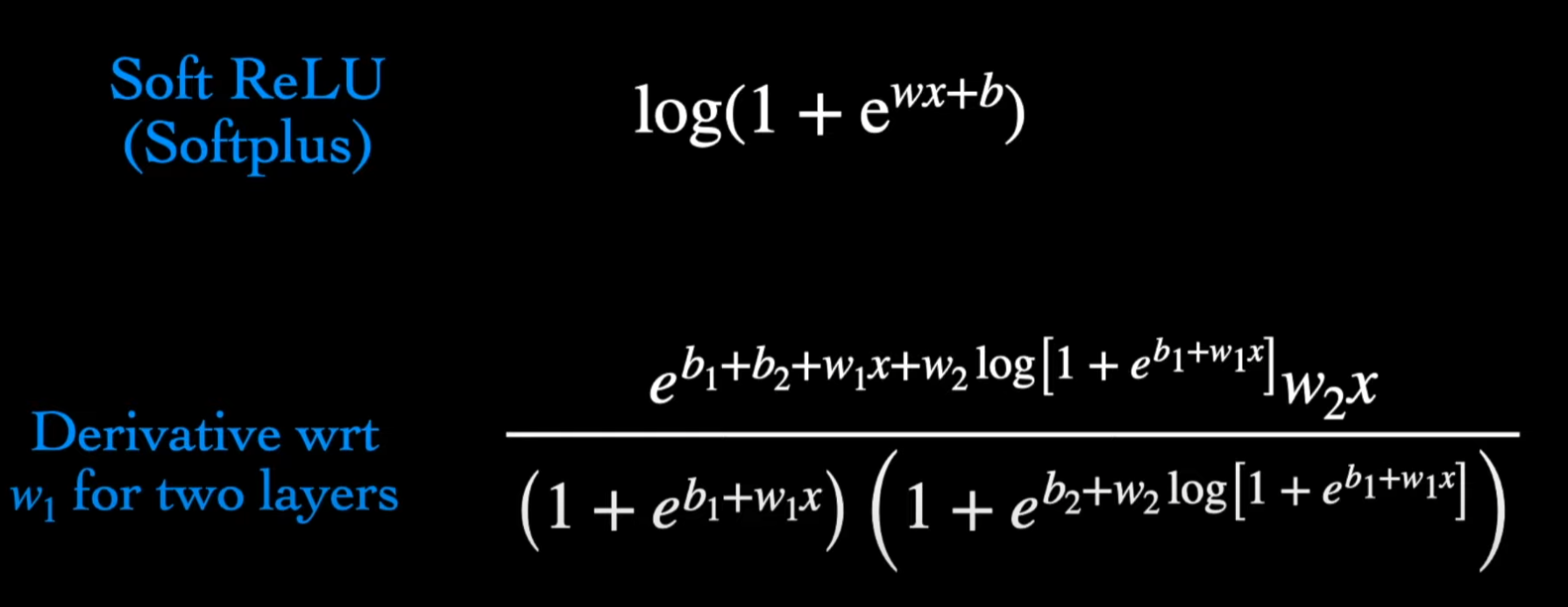
デメリットとして式を展開する必要がありますので、上記通り、複数の関数を合成すると(f ∘ g)計算量・メモリーに対する無理になってしまいます。
更に閉形式の入力が必要となっていますので、IF, FORのようなプログラミングの構造が使えませんのでとても不便です。
- 自動微分 (Automatic differentiation)
自動微分は微分の法則、チェーンルールを利用し、式ではなく値を計算する。
中間値を使って、符号の展開を避けることができますので、精度を守りながら計算量・メモリーに対する要求を減らすことができます。
自動微分はボトムアップ型自動微分 (Forward Autodiff)とトップダウン型自動微分 (Backward/Reverse Autodiff)。
機械学習において、圧倒的に自動微分が使われていますのでこれについて詳しく話したいと思います。
ボトムアップ型自動微分 (Forward Autodiff)
ボトムアップは名前通り、入力から前に進む手法であり、全てfm関数は一つの入力x1に対する微分を計算できる。
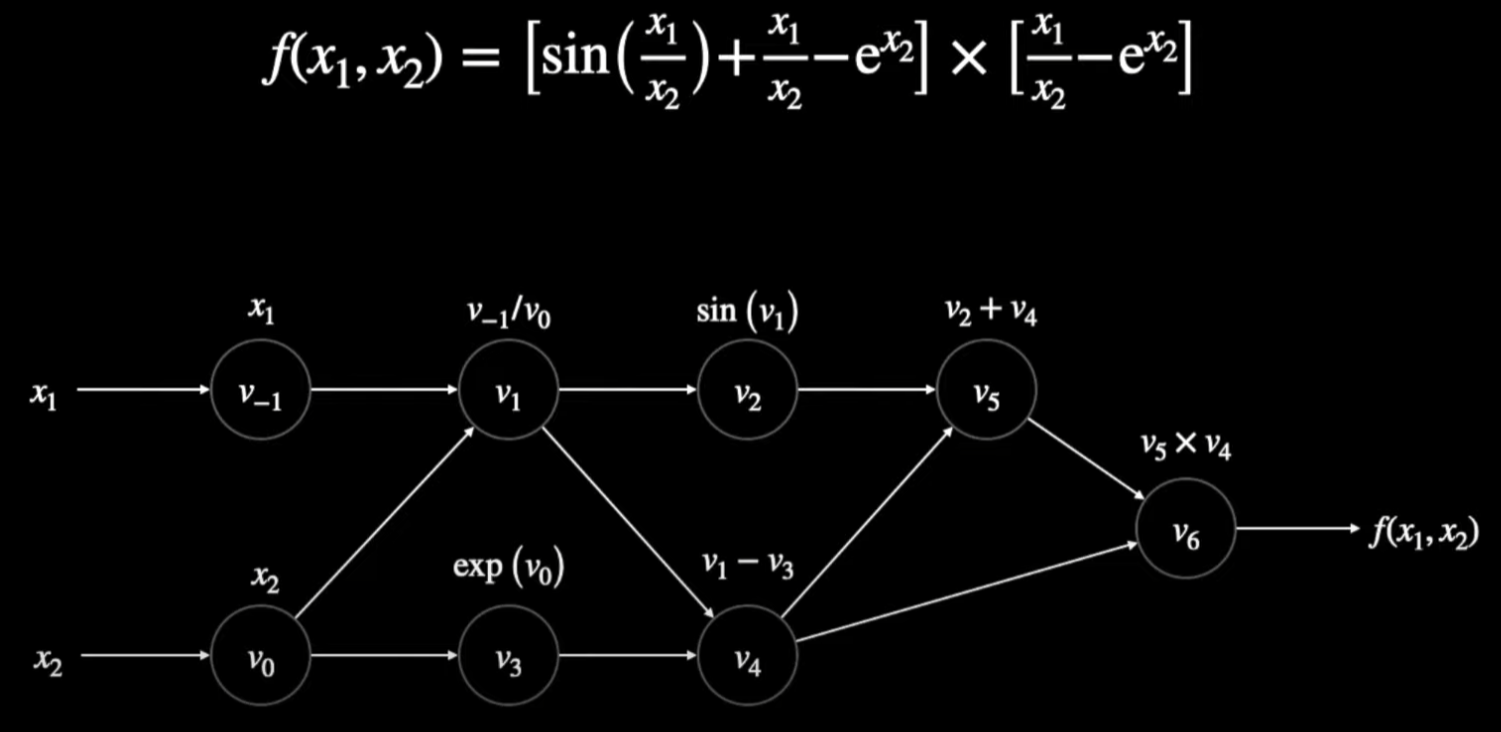
例として、上の関数について以下の微分の計算したい:
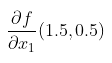
その時、下記の通り、x1とx2の値に決めて、値(primals)と一次微分(tangents)をタプルとして計算する。
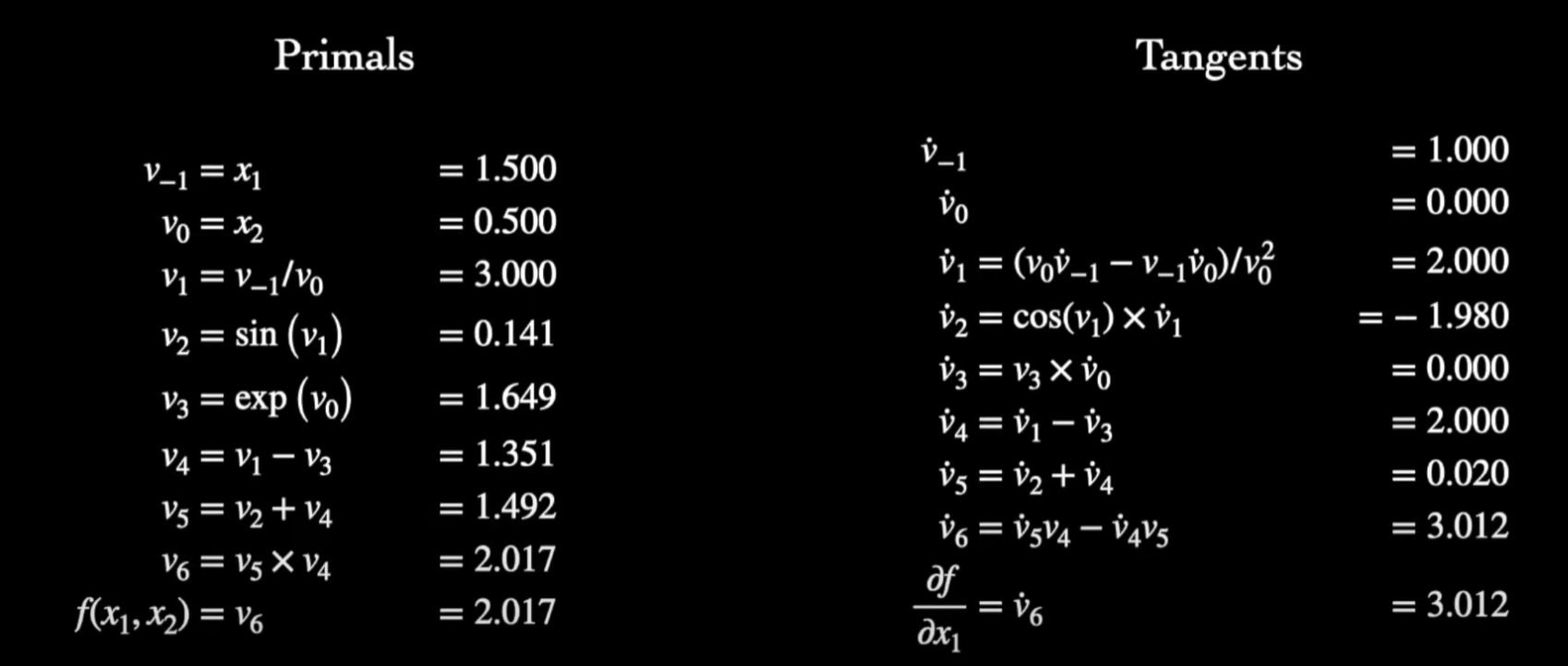
最初のtangentsがx1に対する偏微分になっていますので、最後の結果もfがx1に対する微分になっています。また、複数のfがあってもグラフを通りましたら微分の値を計算できます。
この手法が m >> n の場合だととても良いですが、機械学習において n >> m なので、Backward Autodiffが必要となる。
トップダウン型自動微分 (Backward/Reverse Autodiff)
トップダウンは、出力からの逆計算なっていますが、流れという二つの部分があります。
- まずは一回ボトムアップ型を計算を行う、ただし、一次微分を計算をせずにメモリーに中間値とグラフ関係をセーブする(このデータを「テープ」と呼ぶ)
- 出力からそれぞれのノードのAdjointを計算し、入力まで微分の一々計算する
ちなみに、Define-and-run(TensorFlow, Theanoとdefine-by-run(PyTorch, Chainer)の違いはステップ1にあります:
- (Define-and-run): 最初のForward計算をすると、グラフを全部作ってデータを入れて計算する
- (Define-by-run):データ使って、中間値を計算しながらグラフを作る。
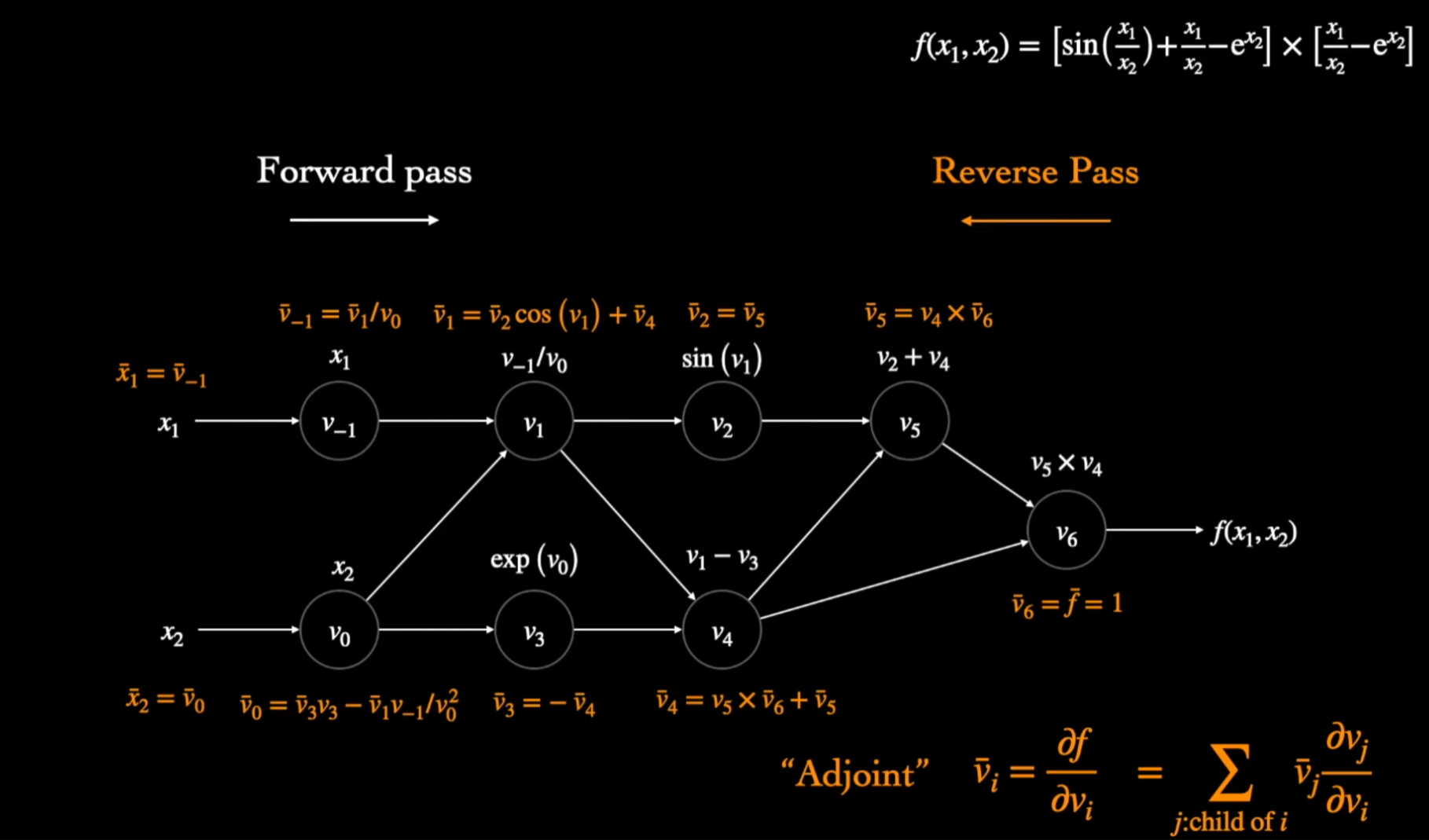
例として、同じ(1.5, 0.5)点で、今回はfがx1とx2に対する微分を計算しましょう。

上の例通り、グラフの一回通りましたらある出力に対して全ての入力の微分を計算できますので、 m << n の場合効率的です。つまり、ニューラルネットワークの話をすると、この自動微分を使っている
実装・機械学習における考慮
時空間計算量
Griewank and Waltherたちがトップダウン型・ボトムアップ型の時空間計算量について以下を証明しました。
| 時間量 | 空間量 | |
|---|---|---|
| Forward | ncops(f) | O(1) |
| Backward | mcops(f) | O(ops(f)) |
ops(f)はグラフを一回評価する計算量
c は係数であり、その値が <= 6、実際に2-3ぐらい。
更に、ボトムアップ型の空間量に対して、グラフのある部分だけをセーブする機能で更に空間量を節約できる論文もあります。
Source code transformation
これは、OOP言語が存在する前にでも存在していた古いアプローチである。要するに、プログラマーは外部のツールを使って、ツールに関数・変数の定義を提供しましたら、ツールが関数を定義するコードを自動的に書いてもらえる。

利点としてはコンパイラーに関数のロジックを直接に見せて、最適化も可能になる。
デメリットとして外部のツールを使う必要があって、人工的に入力する必要があります。
Operating Overloading
Pythonのような言語では変数の値・微分をペアでトラックするクラスを定義し、直接にdunderメソッドによりオペレーターをオーバーロードすることができる。
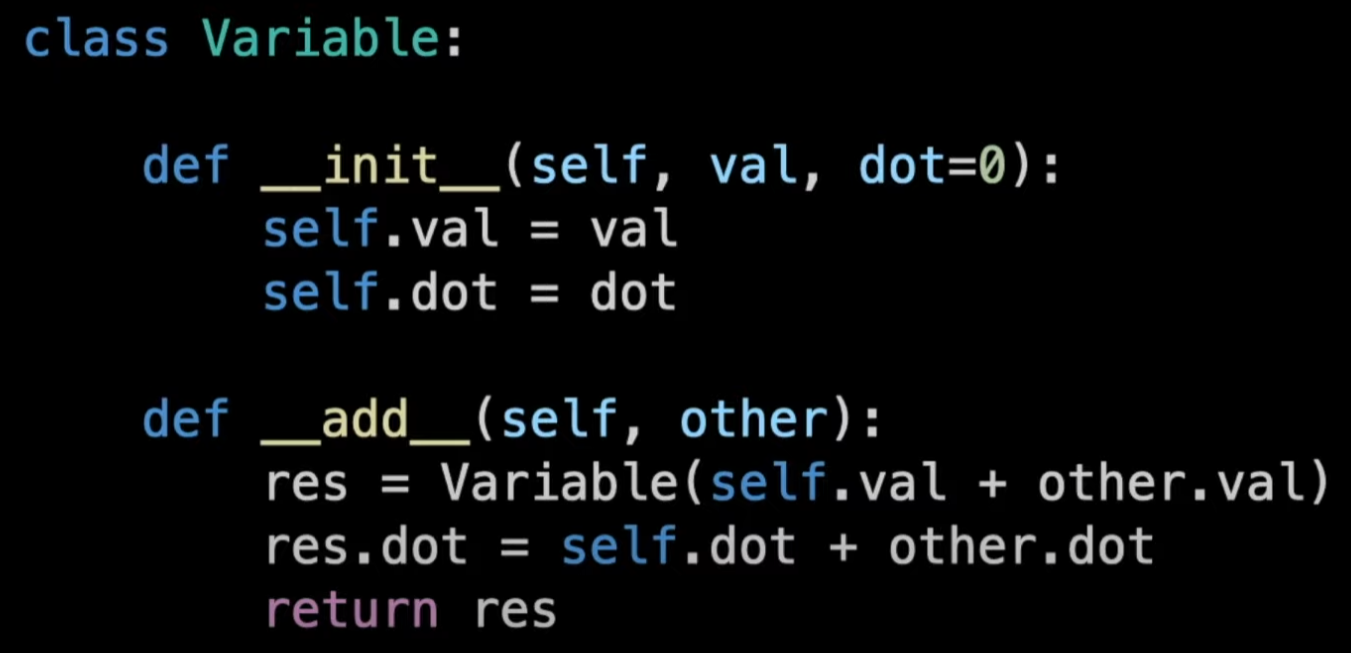
しかし、このようなクラスの定義において、プログラミング言語によって色々な制限がありますのでも完璧なアプローチではありません。
結論
今回はプログラミング言語において微分の実装について紹介しました。また機会がありましたら人気のDLフレームワークにおいてAutodiffの詳細について、Differential Programingというパラダイムについて勉強したいと思います。

